التوازي و التعامد (الأولى إعدادي )1
تذكير
خاصية 1 : من نقطتين مختلفتين A و B يمر مستقيم وحيد نرمز له بالرمز ((AB
ملاحظة :
نرمز للمستقيم أيضا ب : ; (D") ; (L) ; …. (D) ; (D')
تعريف 1 : النقط المستقيمية
نقول عن ثلاث نقط ( أو أكثر ) أنها مستقيمية إذا كانت تنتمي إلى نفس المستقيم .
نصف المستقيم
C ; A ; B نقط تنتمي في هذا الترتيب إلى المستقيم (D)
النقطة A تحدد على المستقيم (D) جزأين . كل جزء منهما يسمى نصف مستقيم أصله A و حامله (D)
نرمز لنصف المستقيم الذي أصله A و يمر من B بالرمز [AB)
و نرمز لنصف المستقيم الذي أصله A و يمر من C بالرمز [AB)
الأوضاع النسبية لمستقيمين في المستوى
المستقيمان المتقاطعان
تعريف 2 : المستقيمان المتقاطعان هما اللذان لهما نقطة وحيدة مشتركة
المستقيمان المتوازيان
تعريف 3 : يكون مستقيمان متعامدان إذا كانا متقاطعين و يحددان زاوية قائمة
المستقيمان المتوازيان
تعريف 4 : المستقيمان المتوازيان هما مستقيمان غير متقاطعان
ملاحظة :
المستقيمان المنطبقان هما أيضا مستقيمان متوازيان
خاصية 2 : من نقطة تنتمي أو لا تنتمي إلى مستقيم (D) يمر مستقيم وحيد على المستقيم (D)
خاصية 3 : من نقطة خارج مستقيم يمر مستقيم آخر يوازيه
المسقط العمودي لنقطة على مستقيم
تعريف 5 : (D) مستقيم و A نقطة خارجه , المسقط العمودي لنقطة A على المستقيم (D) هو نقطة تقاطع (D) و العمودي عليه المار من A .
تعريف 6 : H المسقط العمودي للنقطة A على المستقيم (D) , و المسافة AH تسمى المسافة بين النقطة A و المستقيم (D) .
منصف قطعة
تعريف 7 : نقول أن M منصف [AB] إذا كانت M تنتمي إلى المستقيم (AB) و MA=MB
القطع المتقايسة
تعريف 8 : القطع المتقايسة هي التي لها نفس الطول
الزاوية (الأولى إعدادي )1
نصفا مستقيم [OA) و [OB) يحددان زاويتين , إحداهما تسمى الزاوية المحدبة و نرمز لها بالرمز [AÔB] و الأخرى تسمى الزاوية الغير محدبة و نرمز لها بالرمز [AŎB]
النقطة O تسمى رأس الزاوية [AÔB] (و [AŎB] )
نصف المستقيم [OA) و [OB) يسميان ضلعي الزاوية [AÔB] (و [AŎB] )
قياس زاوية
[AÔB]زاوية قياسها ْ26 درجة AÔB = 26°
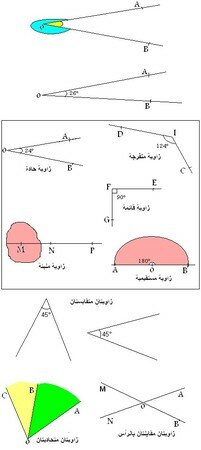
زوايا خاصة
الزاوية الحادة هي كل زاوية قياسها أصغر من 90° درجة
الزاوية المنفرجة هي كل زاوية قياسها محصور بين 90° و 180°
الزاوية المستقيمية هي كل زاوية قياسها 180°
الزاوية المليئة هي كل زاوية قياسها 360°
الزاوية المنعدمة هي كل زاوية قياسها 0°
ملاحظة
ضلعا كل من الزاوية المليئة و الزاوية المنعدمة هما نصفا مستقيم منطبقان
الزاويتان المقايستان
[AÔB] و [CÎD] زاويتان لهما نفس القياس , نقول أنهما متقايستان و نكتب AÔB = CÎD أوAÔB] = [CÎD] ]
تعريف 1 : الزاويتان المتقايستان هما الزاويتان اللتان لهما نفس القياس
الزاويتان المتتامتان
لدينا AÔB = 35°و CÎD= 55°
نلاحظ أن AÔB = 90°+ CÎD
نقول [AÔB] و [CÎD] زاويتان متتامتان
تعريف :90° الزاويتان المتتامتان هما اللتان مجموع قياسهما يساوي
الزاويتان المتكاملتان
لدينا AÔB = 85° و95° = CÎD
AÔB = 180°+ CÎD نلاحظ أن
نقول [AÔB] و [CÎD] زاويتان متكاملتان
تعريف : الزاويتان المتكاملتان هما اللتان مجموع قياسها يساوي 180°
الزاويتان المتحاديتان
الزاويتان [AŎB] و [BÔC] لهما نفس الرأس O و يشتركان في الضلع [OB)
نقول الزاويتان [AŎB] و [BÔC] متحاديتان
تعريف : الزاويتان المتحاديتين هما اللتان لهما نفس الرأس و يشتركان فقط في ضلع واحد
الزاويتان المتقابلتان الرأس
D و (▲) مستقيمان متقاطعان في O
الزاويتان [AÔB] و [MÔN] يسميان زاويتان متقابلتان بالرأس
تعريف : الزاويتان المتقابلتان بالرأس هما اللتان لهما نفس الرأس و ضلعا كل واحدة منهما إمتداد ضلعي الزاوية الأخرى
خاصية : الزاويتان المتقابلتان بالرأس متقايستان
|
أن يطعنك أحدهم في ظهرك فهذا أمر طبيعي ولكن أن تلتفت وتجده أقرب الناس إليك فهذه هي الكارثة
|